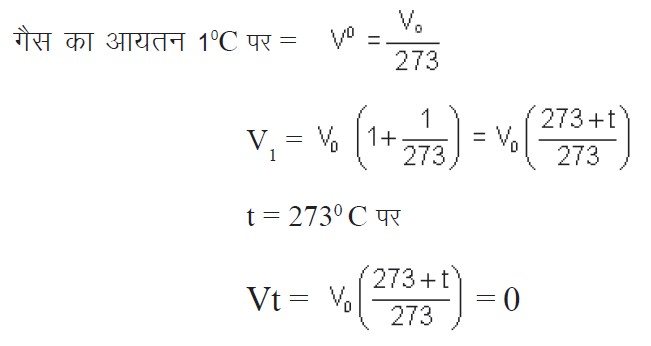गैसीय अवस्था

by admin · July 7, 2019

पदार्थ की तीन भौतिक अवस्थाएँ होती है-ठोस, द्रव तथा गैस। आधुनिक अनुसन्धानों द्वारा Single अवस्था और ज्ञात की गयी है जिसे प्लाज्मा कहते है। ताप तथा दाब की परिस्थितियों के According पदार्थ Single समय में किसी Single भौतिक अवस्था में पाया जाता है। इन तीनों अवस्थाओं में कोर्इ सुस्पष्ट सीमांकन रेखा नहीं होती, किसी भी पदार्थ का ताप, दाब आदि परिवतर्न करके उसे Single अवस्था से दूसरी अवस्था में बदला जा सकता है।

उदाहरणार्थ- जल की तीन अवस्थाएँ होती हैं, जिन्हें केवल ताप परिवर्तन से Single-Second में परिवर्तित Reseller जा सकता है।

बर्फ (ठोस) > 0⁰C जल (द्रव) > 100⁰C जल-वाष्प (गैस)
< 0⁰C < 100⁰

प्रत्येक अवस्था में पदार्थ के कुछ विशेष गुण होते है।

पदार्थ की तीन भैतिक अवस्थाओं की तुलना

गुण	ठोस	द्रव	गैस
कठोरता	इनमें अणु आपस में दृढ़ता से बंधे होते है जिससे ठोस कठोर और नियमित होते है।	इनमें अणु ढीले बंधे होते है जिससे द्रव कड़े नही होते तथा अनियमित होते है।	इनमें अणु काफी दूरी पर रहते है जिससे गैसें मुलायम हल्की तथा अनियमित होती है ।
आकार And आयतनं	प्रबल अंतराआणविक बल के कारण ठोसों के आकार और आयतन दोनो निश्चित होते हैं।	दुर्बल अंतरा आणिवक बल के कारण द्रवों का कोर्इ निश्चित आकारनही होता किन्तु आयतन निश्चित होता है।	अति दुर्बल अंतराआणविक बल के कारण आकार और आयतन दोनो अनिश्चित होते हैं ।
क्रिस्टल जालक	इनमें अणुओं की स्थिति निश्चित होती है, अत: क्रिस्टल जालक बनाते है।	इनमें अणुओं की स्थिति निश्चित होती है जिससे इनकी क्रिस्टलीय संCreation नहीं होती।	इनके अणु अत्यंत गतिशील होते है अत: क्रिस्टल जालक बनने की कोर्इ संभावना नही होती है।
विसरण	विसरण नही करते।	आंशिक विसरण करते है।	इनकी मुक्त गति के कारण अधिकतम विसरण होता है।
संपीड़यता	अंतराआणविक स्थान कम से कम होने के कारण असंपीड्य है।	अंतराआणविक स्थान ठोसों की अपेक्षा अधिक होने के कारण संपीड्य हैं।	अधिकतम अंतराआणविक स्थान पाये जाने के कारण गैसे अधिकतम संपीड्य है।
गतिजऊर्जा	इनके अणुओं की गतिज ऊर्जा न्यूनतम होती है।	इनके अणुओं की गतिज ऊर्जा ठोसों से अधिक किन्तु गैसों स कम होती है।	इनकी गतिज ऊर्जा ठोस और द्रवों की तुलना में काफी अधिक होती है।

द्रव्य की तीनों अवस्थाओं के उपर्युक्त गुणधर्म कणों की आपेक्षिक निकटता पर निर्भर करते है। ठोसो में अंत: अणुक बल प्रबल होते है जो कणो को पास-पास और अपने स्थान पर स्थिर रखते है। द्रवों में अंत: अणुक बल ठोसो की तुलना में दुर्बल होते है इसलिए वे बहुत पास नहीं होते और Single सीमा में गतिशील होते है। गैसीय अवस्था में अंत: अणुक बल इसलिए कण सतत अनियमित गति से चलते है। ठोस, द्रव और गैसीय कणों की सरलीकृत व्यवस्था चित्र में दी गर्इ है।

(चित्र- ठोस, द्रव, गैसीय अवस्थामें कणो का Single सरलीकृत चित्रण)

गैसो का सामान्य व्यवहार

द्रव्य (पदार्थ) की तीनों अवस्थाओं में से गैसीय अवस्था का व्यवहार सरल तथा समरूम (uniform) होता हैं। All गैसों का व्यवहार लगभग Singleसमान ही होता हैं तथा उनकी रासायनिक प्रकृति पर निर्भर नहीं होता।

गैसीय अवस्था की विशेषताएँ –

आकार- यह द्रव्य की सबसे अधिक अव्यवस्थित अवस्था हैं। गैस में अणुओं का स्थान निश्चित नहीं होता । वह पात्र के सम्पूर्ण आयतन में व्याप्त हो जाता है। अत: गैस का कोर्इ निश्चित आकार नहीं होता है।
आयतन- गैस का आयतन ताप, दाब और पात्र पर निर्भर करता है। अत: अनिश्चित होता है।
गतिज ऊर्जा- गैस के अणुओं में स्थानान्तरण, घूर्णन तथा कम्पन्न तीनों प्रकार की गति सम्भव है फलस्वReseller गैसीय अणुओं की गतिज ऊर्जा उच्च होती है।
सम्पीड्यता-गैसों में अत्यधिक सम्पीड्यता पायी जाती है।
प्रसार- गैसों का प्रसार असीमित होता है। गैसें अपनें को समाहित करने वाले पात्र के सम्पूर्ण आयतन को घेर लेती हैं।
दाब-गैसे अपने को समाहित करने वाले पात्र की आन्तरिक दीवारों पर दाब उत्पन्न करती हैं। यह दाब गैसीय अणुओं के पास की दीवारों से टकराने के कारण होता है।
घनत्व-गैसों का घनत्व अत्यन्त कम होता है क्योकि गैसीय अणुओं में अन्तराअणुक स्थान अधिक तथा अन्तराअणुक आकर्शण बहुत कम (नगण्य) होता है।
विसरण-गैसें सरलता से विसरित हो जाती हैं तथा आपस में मिलकर समांगी मिश्रण बनाती है।
द्रवण-प्राय: All गैसें निम्न ताप पर द्रवित हो जाती हैं। ताप कम होने पर गैसों के अणुओं की गतिज ऊर्जा कम हो जाती हैं, अणु पास – पास आ जाते हैं तथा अन्तराअणुक आकर्षक बढ़ जाता है।

गैस के नियम

किसी गैस के लिए द्रव्यमान तथा आयतन उस ताप और दाब पर निर्भर करेगा, जिस पर वह गैस पार्इ जाती है। अत: गैसो के व्यवहार का History चार चरों : ताप T, दाब च्ए आयतन V और मात्रा (मोलो की संख्या, n) के Reseller मे Reseller जाता है। किसी गैस की दी गर्इ मात्रा के लिए ताप और दाब जैसे चरो में परिवर्तन करने पर आयतन बदल जाता हैं । दो चरो के पारस्परिक अध्ययन के लिए अन्य चरो को स्थिर रखा जाता है। यहाँ हम गैसीय नियमों का अध्ययन करेगें।

1. आयतन पर दाब का प्रभाव (बॉयल का नियम)

सन् 1662 में राबर्ट बॉयल ने विभिन्न गैसों के लिए स्थिर ताप पर दी गर्इ गैस की मात्रा के आयतन पर दाब के प्रभाव का अध्ययन Reseller । उसने पाया कि गैस का आयतन दुगना करने पर दाब आधा रह जाता है और बदले क्रम में भी यही परिणाम मिले। बॉयल नियम के According-स्थिर ताप पर किसी गैस के लिए दिए हुए द्रव्यमान का आयतन दाब का व्युत्क्रमानुपाती होता है।

गणितीय रूम में
V a 1/p (स्थिर T और n पर )
अथवा P₁ V₁ = P₂ V₂

ताप को स्थिर रखते हुए यदि किसी गैस के आयतन V को दाब के साथ आलेखित Reseller जाए तो चरघातांकी ग्राफ प्राप्त होगा।

अगर दाब P को आयतन के व्युत्क्रम, 1/v के साथ आलेखित Reseller जाए तो मूल बिन्दु से गुजरता हुआ ऋजु रेखी ग्राफ प्राप्त होता है। दाब और आयतन के गुणनफल (pV) को दाब (p) के साथ आरेखित करने से x – अक्ष के समान्तर Single ऋजु रेखा मिलती है।

2. आयतन पर ताप का प्रभाव (चाल्र्स नियम)

सन् 1787 में जैक्स चाल्र्स और 1802 में गैलुसैक ने स्थिर दाब पर विभिन्न गैसों के आयतन पर ताप के प्रभाव का अध्ययन Reseller।

चाल्र्स का नियम तथा ताप का परम मापक्रम

ताप का परम मापक्रम

फ्रांस के रासायनज्ञ जे.. चाल्र्स (सन् 1787) और गे- लुसाक (सन् 1802) ने अपने- अपने प्रयोगो में पाया कि ‘‘स्थिर दाब पर किसी गैस के निश्चित द्रव्यमान का आयतन 10C ताप की वृध्दि या कमी से अपने 00C वाले आयतन के 1/273 या 0. 00366 वें भाग से बढ़ता या घटता है।’’

मानलो किसी गैस के निश्चित द्रव्यमान का किसी निश्चित दाब पर 0 C पर आयतन V0 तथा t0C पर आयतन Vt है। अत: चालर्स और गे-लुसाक के प्रेक्षणों के According,

Meansात्- 2730C पर किसी भी गैस का आयतन शून्य हो जाता है (कोर्इ भी गैस Single द्रव्य है, इसका कुछ द्रव्यमान होता है अत: आयतन शुध्द Reseller से शून्य नही हो सकता)। यह ताप, जिस पर गैस का आयतन शून्य हो जायेगा ताप का परम शून्य (Absolute zero temperature) कहलाता है। यह वह निम्नतम ताप है जिस पर कोर्इ गैस सैध्दान्तिक Reseller से उपस्थित रह सकती है, किन्तु वास्तविक में कोर्इ भी गैस इस ताप के First ही द्रव या ठोस में परिवर्तित हो जाती है। इस शून्य से ताप का स्केल चुनने पर यह स्केल ताप का परम स्केल (absolute scale of temperature) कहलाता है। इस स्केल को सबसे First ब्रिटिश वैज्ञानिक लार्ड केल्विन ने सुझाया अत: इसे केल्विन स्केल (Kelvin scale) भी कहा जाता है।

केल्विन स्केल के ताप को दर्शाने के लिए संकेत K का उपयोग करते है तथा उसमें डिग्री ( 0 ) का चिन्ह नही लगाया जाता है। अत:

  -273.150C = 0 K
  या 0oC = 273.15K
  या 0o C = 273
  K roC = (273 + t)
  K toC = TK (सरलता के लिए)

जिसमें t सेल्सियम स्केल पर तथा T केल्विन स्केल पर ताप है। अत: केल्विन स्केल से ताप का मान ज्ञात करने के लिए सेल्सियम स्केल के ताप में 273.15 (अथवा 273) जोड़ दिया जाता है।

T (K) = t0 (C) + 273

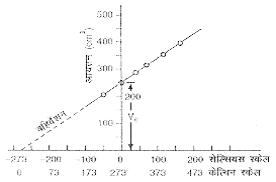
यदि ताप t का X- अक्ष पर तथा आयतन V को Y- अक्ष पर लेकर Single ग्राफ खीचा जाय तो चित्रानुसार Single सरल रेख प्राप्त होती है इस सरल रेखा का बहिर्वेशन (extrapolation) करने पर वह ताप अक्ष को जिस ताप पर छूती है वहां गैस के आयतन का मान शून्य होता है। वह ताप जिस पर गैस का आयतन शून्य हो जाता है -273.15oC पाया गया है । यहॉ पर यह बात ध्यान देने योग्य है कि ताप का यह मान Meansात -273.15oC गैस को प्रकृती पर निर्भर नही होता।

चाल्र्स नियम

यह नियम स्थिर दाब पर गैसो के आयतन पर ताप के प्रभाव को परिभाशित करता है।

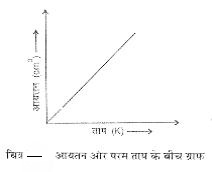
किसी गैस की निश्चित मात्रा का आयतन सेल्सियस स्केल के ताप का रैखिक फलन (Linear function) है परन्तु इससे यह पता लगता है कि स्थिर दाब पर आयतन ताप के अनुक्रमानुपाती है । यदि ताप को केल्विन स्केल में दर्शाया जावे अैार आयतन को cm3 में तो प्राप्त वक्र Single सरल रेखा होता है जिसका बहिर्वेशन (extrapolation) करने पर मूल बिन्दू में जाता है। ताप (K) और आयतन (cm3) का ग्राफ देखिए।

अत: V = T
अथवा V = स्थिरांक × T (दाब तथा द्रव्यमान की मात्रा स्थिर पर)
अथवा = स्थिरांक

चाल्र्स नियम के According, ‘‘स्थिर दाब पर निश्चित द्रव्यमान की गैस का आयतन केल्विन स्केल के ताप के अनुक्रमानुपाती होती है।’’

चाल्र्स नियम के समीकरण का सरल Reseller निम्न है –

V1 T1
–– = –– (निश्चित द्रव्यमान तथा दाब पर)
V1 T1

जिसमें V1 प्रारंभिक आयतन, T1 प्रारंभिक परमताप V2 अन्तिम आयतन तथा T2 अन्तिम परम ताप है। यदि कोर्इ तीन परिवर्ती ज्ञात हों तो Fourth का निर्धारण Reseller जा सकता है।

चार परिवर्तियों (Meansात् V1 , V2 , T1 तथा T2 ) का यह समीकरण गणनाओं के लिए उपयुक्त है, क्योंकि यदि कोर्इ तीन परिवर्ती ज्ञात हों तो Fourth का निर्धारण Reseller जा सकता है।

चाल्र्स के नियम का प्रायोगिक महत्व-

खेलों के लिए तथा मौसम विज्ञान सम्बन्धी प्रयोगों के लिए प्रयुक्त होने वाले गर्म वायु के गुब्बारे चाल्र्स के नियम पर आधारित है। गैसें गर्म करने पर फैलती है तथा गर्म वायु कम सघन है इसलिए गर्म वायु का बैलून ठण्डे (अधिक सघन) वायुमण्डल की वायु को विस्थापित करके ऊपर उठता है।

3. ताप का दाब पर प्रभाव ( गे-लुसाक का नियम)

गे-लुसाक का नियम स्थिर आयतन पर गैसों के दाब And ताप के मध्य सम्बन्ध प्रतिपादित करता है। इस नियम के According ‘‘किसी गैस की निश्चित मात्रा का आयतन स्थिर रखने पर उसका दाब परम ताप के अनुक्रमानुपाती होता है।’’

  अत: P ∞ T
  या P = स्थिरांक × T
  या P/T= स्थिरांक

स्थिरांक का मान गैस के द्रव्यमान और आयतन पर निर्भर होता है।

विभिन्न गैसों के दाब और परम ताप के मध्य, निर्धारित मापदण्ड से, ग्राफ खीचने पर सरल रेखाएँ प्राप्त होती हैं। (चित्र ) इससे गे-लुसाक के नियम को बल मिलता है। यदि P1 , T1 , P2 और T2 किसी गैस के लिए क्रमश: प्रारम्भिक दाब, प्रारम्भिक परम ताप, अन्तिम दाब और अन्तिम परम ताप हों,

तो-
  P1
  ––– = K (निश्चित द्रव्यमान तथा स्थिर आयतन पर)
  T1
And =    P1
    ––– = K (स्थिराक)
     T1
इसलिए P1 P2
     ––– = –––……….=(स्थिराक)
      T1 T2

स्थिरांक यह गे-लुसाक समीमकरण है।

4. आवोगाद्रो नियम

इटली के भौतिकविद अमैदिओ आवोगाद्रो First व्यक्ति थे जिन्होंने सन् 1811 में गैस के आयतन और उसमें विद्यमान अणुओं की संख्या के बीच संबंध प्रस्तुत Reseller। इस संबंध को आवोगाद्रो नियम कहते है,
इसके According-
‘‘सामान्यत: ताप और दाब पर गैसो के बराबर आयतनों में अणुओं की संख्या बराबर होती है।’’
गणितीय Reseller :

V a N (स्थिर ताप और दाब पर )

यहाँ V और N क्रमश: आयतन और अणुओं की संख्या हैं।
‘‘दिए गए ताप और दाब पर गैस में उपस्थित अणुओं की संख्या, मोलों की संख्या के समानुपाती होती है’’
अत: N n
यहाँ n मोलो की संख्या है।
V = n
अथवा V/n स्थिरांक
इसलिए = V1 V2
––– = –––……….=(स्थिराक)
n1 n2

इन्होने किसी पदार्थ के Single मोल में अणुओं की संख्या भी दी जोकि 6.022× 1023 है। इसे आवोगाद्रो संख्या भी कहते हैं।